A matemática
está presente em boa parte da nossa vida é só você reparar. E se você reparar
bem poderá vê-la nos momentos e lugares mais inusitados. Como no sofrimento do
jogo do Brasil na Copa do mundo, no jogo contra o Chile, que foi para a
cobrança de pênaltis. A última cobrança do Chile em relação ao goleiro Júlio
César e a trave tiveram uma angulação e esse pênalti parou na trave. Que
angulação foi essa? E pra que a bola pudesse ter entrado que angulação
precisaria?
A trave tem
um comprimento de 7,32m,então onde o goleiro fica que é o centro até uma das
trave mede 3,66m e a marca do pênalti até o gol tem uma distância de 11m, então
vamos encontrar a distância do jogador Jara até a trave direita e depois
usaremos Lei dos Senos para saber o ângulo do Vértice B como mostra a figura 1.
Sabendo que o ângulo do
vértice M é de 90° vamos descobrir o ângulo do vértice B usando lei dos senos.
Com essa angulação a
bola do jogador Jara do Chile bateu na trave. Vamos ver agora que angulação precisaria
para a bola ter entrado e continuar o sofrimento de todos os Brasileiros. Para
que a bola entre vamos “afastar” ela para a esquerda. Então a distância do
centro do gol até a bola vai diminuir. A circunferência da bola mede 70 cm,e a metade (que é o que precisamos) mede 35cm. Diminuindo da distância que tínhamos de 3,66m do centro do gol até a trave
(onde a bola bateu) temos agora uma distância de 3,31m. Como mostra figura 2.
Fazendo um novo cálculo
para encontrar a nova hipotenusa e depois o ângulo do vértice B para que a bola
fosse gol, Temos:
Com essa angulação a
bola do Jara teria entrado e os Brasileiros continuariam com o seu sofrimento.
Viu galera? Até nos
nossos sofrimentos existe 'Trigonometria' hehe.


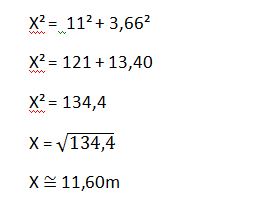





Exemplo excelente... Agora, uma pergunta... Você precisa da circuferência máxima da bola (esfera) ou do seu diâmetro?
ResponderExcluir